Post

Using Z3 in Reverse Engineering

Posted Updated
Preview Image
By Anish Kumar Roy
24 min read

Z3 is primarily a theorem prover and Satisfiability Modulo Theories (SMT) solver, developed at Microsoft Research. It is capable of solving first-order logic problems, making it suitable for a wide range of applications in software verification.

Installing Z3

To use the python module you need to install z3-solver

1

pip install z3-solver

Some basic functions in Z3 that you need to know about

BitVec : It creates a variable (whose value we need to find), with a specific size that we mention.
Solver : It initializes a solver instance to which constraints can be added, using Solver.add().
Solver.check() : It checks the satisfiability of the problem. If a solution is found, then it retuns sat otherwise it returns unsat.
Model : If satisfiable Solver.Model() retrieves a model satisfying the constraints.

Let’s dive into some examples too understand it better.

Example 1

This is a reverse engineering challenge from the Anveshanam CTF

You can acess the challenge file here
We are given a challenge that says -

desc

On opening the binary in Ghidra 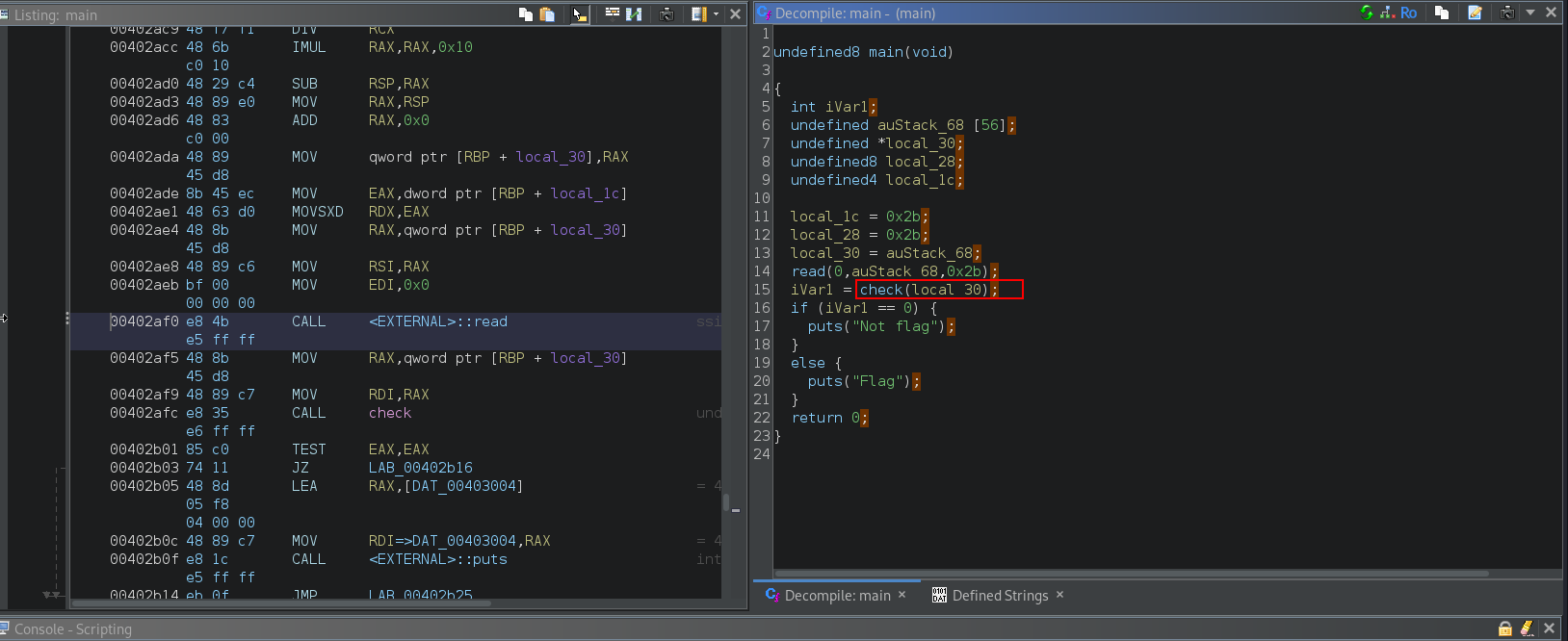check As we can see, our input is being passed onto the check function. If the return value is not equal to zero then it says Flag So, we need to determine the correct input. For that let’s view the check function - 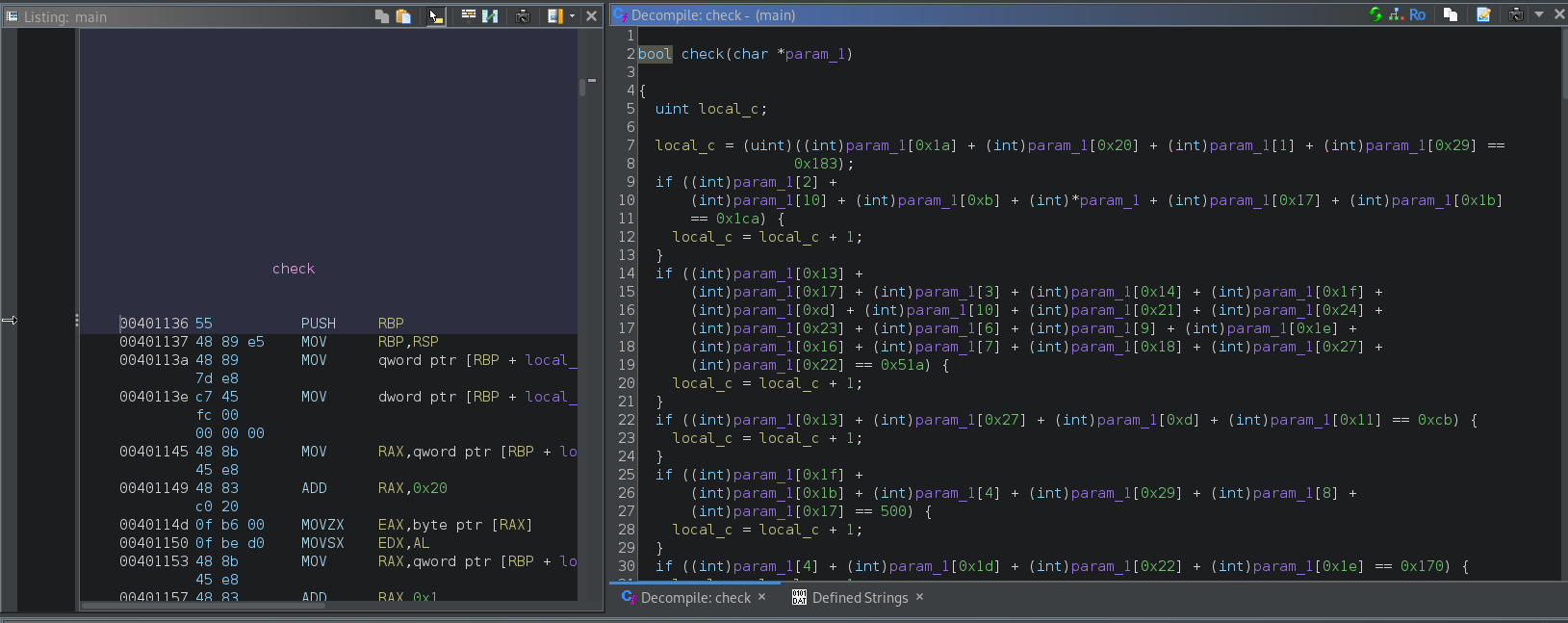check1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222

bool check(char *param_1)

{
  uint local_c;
  
  local_c = (uint)((int)param_1[0x1a] + (int)param_1[0x20] + (int)param_1[1] + (int)param_1[0x29] ==
                       0x183);
  if ((int)param_1[2] +
       (int)param_1[10] + (int)param_1[0xb] + (int)*param_1 + (int)param_1[0x17] + (int)param_1[0x1b]
       == 0x1ca) {
     local_c = local_c + 1;
  }
  if ((int)param_1[0x13] +
       (int)param_1[0x17] + (int)param_1[3] + (int)param_1[0x14] + (int)param_1[0x1f] +
       (int)param_1[0xd] + (int)param_1[10] + (int)param_1[0x21] + (int)param_1[0x24] +
       (int)param_1[0x23] + (int)param_1[6] + (int)param_1[9] + (int)param_1[0x1e] +
       (int)param_1[0x16] + (int)param_1[7] + (int)param_1[0x18] + (int)param_1[0x27] +
       (int)param_1[0x22] == 0x51a) {
     local_c = local_c + 1;
  }
  if ((int)param_1[0x13] + (int)param_1[0x27] + (int)param_1[0xd] + (int)param_1[0x11] == 0xcb) {
     local_c = local_c + 1;
  }
  if ((int)param_1[0x1f] +
       (int)param_1[0x1b] + (int)param_1[4] + (int)param_1[0x29] + (int)param_1[8] +
       (int)param_1[0x17] == 500) {
     local_c = local_c + 1;
  }
  if ((int)param_1[4] + (int)param_1[0x1d] + (int)param_1[0x22] + (int)param_1[0x1e] == 0x170) {
     local_c = local_c + 1;
  }
  if ((int)param_1[0x25] +
       (int)param_1[0x24] + (int)param_1[0x23] + (int)param_1[0x29] + (int)param_1[0xf] +
       (int)param_1[0x15] + (int)param_1[0x28] + (int)param_1[0x1c] + (int)param_1[0x1a] +
       (int)param_1[0x21] == 0x2fe) {
     local_c = local_c + 1;
  }
  if ((int)param_1[0x15] +
       (int)param_1[6] + (int)param_1[10] + (int)param_1[0xb] + (int)param_1[0xf] + (int)param_1[9] +
       (int)param_1[0x1b] + (int)param_1[3] + (int)param_1[0x1b] + (int)param_1[2] +
       (int)param_1[0x26] == 0x33d) {
     local_c = local_c + 1;
  }
  if ((int)param_1[0x1e] +
       (int)param_1[0x1e] + (int)param_1[0x23] + (int)param_1[0x27] + (int)param_1[0x19] +
       (int)*param_1 + (int)param_1[0x29] + (int)param_1[0x16] + (int)param_1[0x17] + (int)param_1[2]
       + (int)*param_1 + (int)param_1[0xb] + (int)param_1[0x21] + (int)param_1[0xc] + (int)param_1[2]
       + (int)param_1[0x28] + (int)param_1[0x15] + (int)param_1[0x1c] + (int)param_1[1] +
       (int)param_1[0x16] == 0x65f) {
     local_c = local_c + 1;
  }
  if ((int)param_1[0xb] +
       (int)param_1[0x1e] + (int)param_1[0x17] + (int)param_1[0x21] + (int)param_1[0x24] +
       (int)param_1[0xc] + (int)*param_1 + (int)param_1[0x23] + (int)*param_1 + (int)param_1[3] +
       (int)param_1[0xb] + (int)param_1[0x21] + (int)param_1[8] + (int)param_1[0x22] +
       (int)param_1[0xf] + (int)param_1[0x1f] + (int)param_1[2] == 0x57d) {
     local_c = local_c + 1;
  }
  if ((int)param_1[0x22] +
       (int)param_1[0x21] + (int)param_1[0x29] + (int)param_1[8] + (int)param_1[0x29] +
       (int)param_1[5] + (int)param_1[0x10] == 0x289) {
     local_c = local_c + 1;
  }
  if ((int)param_1[0x1b] +
       (int)param_1[0x24] + (int)param_1[8] + (int)param_1[3] + (int)param_1[4] + (int)param_1[0x1c]
       + (int)param_1[0x23] + (int)param_1[0x23] + (int)param_1[0x19] + (int)param_1[0x15] +
       (int)param_1[0x16] + (int)param_1[0x28] == 0x373) {
     local_c = local_c + 1;
  }
  if ((int)param_1[0x1d] +
       param_1[0x22] * 2 + (int)param_1[0xe] + (int)param_1[0x29] + (int)param_1[0x1e] +
       (int)param_1[0x22] + (int)param_1[0xc] + (int)param_1[0xc] + (int)param_1[0x20] +
       (int)param_1[0x23] + (int)param_1[0xc] + (int)param_1[1] + (int)param_1[1] +
       (int)param_1[0x1c] + (int)param_1[0x10] == 0x572) {
     local_c = local_c + 1;
  }
  if ((int)param_1[9] + (int)param_1[0x14] + (int)param_1[6] + (int)param_1[1] == 0x16c) {
     local_c = local_c + 1;
  }
  if ((int)param_1[0x1c] + (int)param_1[9] == 0x65) {
     local_c = local_c + 1;
  }
  if ((int)param_1[0x25] +
       (int)param_1[10] + (int)param_1[0x10] + (int)param_1[0x20] + (int)param_1[0x27] +
       (int)param_1[1] + (int)param_1[0x27] + (int)param_1[9] + (int)param_1[0x29] +
       (int)param_1[0x16] + (int)param_1[0xf] + (int)param_1[0x29] + (int)param_1[0xf] +
       (int)param_1[0x20] + (int)param_1[0xb] + (int)param_1[0x17] + (int)param_1[0x21] +
       (int)param_1[0x25] == 0x5f2) {
     local_c = local_c + 1;
  }
  if ((int)param_1[4] +
       (int)param_1[0x17] + (int)param_1[0x11] + (int)param_1[0x15] + (int)param_1[0x1b] +
       (int)param_1[2] + (int)param_1[0x1d] + (int)param_1[1] + (int)param_1[0x1d] +
       (int)param_1[0x12] + (int)param_1[0x10] + (int)param_1[0xc] + (int)param_1[0x11] +
       (int)param_1[0x24] + (int)param_1[0x13] == 0x3cb) {
     local_c = local_c + 1;
  }
  if ((int)param_1[10] + (int)param_1[10] + (int)param_1[0x25] + (int)param_1[0xd] == 0x156) {
     local_c = local_c + 1;
  }
  if ((int)param_1[8] +
       (int)param_1[0xb] + (int)param_1[0x29] + (int)param_1[0x1d] + (int)param_1[0x12] +
       (int)param_1[0xc] + (int)param_1[0x29] == 600) {
     local_c = local_c + 1;
  }
  if ((int)param_1[8] +
       (int)param_1[0x21] + (int)param_1[6] + (int)param_1[0x14] + (int)param_1[0x20] +
       (int)param_1[0x1d] + (int)param_1[0x28] + (int)param_1[0x16] + (int)param_1[0x11] +
       (int)param_1[0x13] + (int)param_1[0x24] + (int)param_1[0x25] + (int)param_1[0x1d] +
       (int)*param_1 + (int)param_1[0x16] + (int)param_1[9] + (int)param_1[0x1b] == 0x4e7) {
     local_c = local_c + 1;
  }
  if ((int)*param_1 +
       (int)param_1[3] + (int)param_1[0x20] + (int)param_1[0xb] + (int)param_1[4] +
       (int)param_1[0x1e] == 0x247) {
     local_c = local_c + 1;
  }
  if ((int)param_1[0x1b] +
       (int)param_1[0x21] + (int)param_1[0x20] + (int)param_1[0x1c] + (int)param_1[0x25] +
       (int)param_1[0x29] + (int)param_1[0x28] + (int)param_1[0x15] == 0x2a0) {
     local_c = local_c + 1;
  }
  if ((int)param_1[0x15] + (int)param_1[0x10] + (int)param_1[0x1e] + (int)param_1[0x27] == 0x100) {
     local_c = local_c + 1;
  }
  if ((int)param_1[0x23] +
       (int)param_1[5] + (int)param_1[0x20] + (int)param_1[0x28] + (int)param_1[0x10] == 0x162) {
     local_c = local_c + 1;
  }
  if ((int)param_1[0x1e] +
       (int)param_1[8] + (int)param_1[0xb] + (int)param_1[0x1d] + (int)param_1[0x1f] +
       (int)param_1[6] == 0x1c5) {
     local_c = local_c + 1;
  }
  if ((int)param_1[0x29] + (int)param_1[0x24] == 0xad) {
     local_c = local_c + 1;
  }
  if ((int)param_1[10] + (int)param_1[0x15] + (int)param_1[0x14] + (int)param_1[0xc] == 0x15d) {
     local_c = local_c + 1;
  }
  if ((int)param_1[5] + (int)param_1[0x1c] == 0x5e) {
     local_c = local_c + 1;
  }
  if ((int)param_1[1] +
       (int)param_1[0x18] + (int)param_1[0x29] + (int)param_1[4] + (int)param_1[1] + (int)param_1[2]
       + (int)param_1[0x18] + (int)param_1[9] + (int)param_1[0x1c] + (int)param_1[0xd] +
       (int)param_1[0x26] + (int)param_1[0x21] + (int)param_1[0x1c] + (int)param_1[0x26] +
       (int)param_1[7] + (int)param_1[0x19] + (int)*param_1 + (int)param_1[9] + (int)param_1[0x1d] +
       (int)param_1[0xc] == 0x64e) {
     local_c = local_c + 1;
  }
  if ((int)param_1[0x28] +
       (int)param_1[9] + (int)param_1[0x18] + (int)param_1[0x10] + (int)param_1[0xf] +
       (int)param_1[9] + (int)param_1[0x22] + (int)param_1[0xb] + (int)param_1[0x23] +
       (int)param_1[0x21] + (int)param_1[0x21] + (int)param_1[2] + (int)param_1[0x1a] +
       (int)param_1[0x11] + (int)param_1[8] == 0x48c) {
     local_c = local_c + 1;
  }
  if ((int)param_1[2] +
       (int)param_1[2] + (int)param_1[0x12] + (int)param_1[0x1b] + (int)param_1[0x12] +
       (int)param_1[0x10] + (int)param_1[0x29] + (int)param_1[2] + (int)param_1[0x24] +
       (int)param_1[2] + (int)param_1[0x16] + (int)param_1[0x16] == 0x35c) {
     local_c = local_c + 1;
  }
  if ((int)param_1[0xd] + (int)param_1[0xe] + (int)param_1[0xd] == 0x93) {
     local_c = local_c + 1;
  }
  if ((int)param_1[5] +
       (int)param_1[0x1b] + (int)param_1[0x18] + (int)param_1[0x26] + (int)param_1[0x27] +
       (int)param_1[0x28] + (int)param_1[0x16] + (int)param_1[0x28] == 0x232) {
     local_c = local_c + 1;
  }
  if ((int)param_1[0x1e] +
       (int)param_1[0x1a] + (int)param_1[9] + (int)param_1[0x1c] + (int)param_1[0x14] +
       (int)param_1[0xf] + (int)param_1[0x12] + (int)param_1[2] + (int)param_1[0x1a] +
       (int)param_1[5] + (int)param_1[0x1e] == 0x315) {
     local_c = local_c + 1;
  }
  if ((int)param_1[0x17] +
       (int)param_1[0x20] + (int)param_1[0x13] + (int)param_1[0x15] + (int)param_1[2] +
       (int)param_1[0x1c] + (int)param_1[0x1b] + (int)param_1[0x1b] + (int)param_1[2] +
       (int)param_1[0x27] + (int)param_1[0x13] + (int)param_1[0x27] + (int)param_1[0x10] +
       (int)param_1[2] + (int)param_1[2] + (int)param_1[0x18] + (int)param_1[1] + (int)param_1[0x1f]
       + (int)param_1[9] == 0x52d) {
     local_c = local_c + 1;
  }
  if ((int)param_1[0xc] +
       (int)param_1[0x26] + (int)param_1[10] + (int)param_1[0x14] + (int)param_1[0x28] +
       (int)param_1[0x1d] + (int)param_1[0x26] + (int)param_1[0x1a] + (int)param_1[0x1a] +
       (int)param_1[0x1f] + (int)param_1[0x25] + (int)param_1[0x14] + (int)param_1[0xe] +
       (int)param_1[10] + (int)param_1[0x11] + (int)param_1[0x26] + (int)param_1[0x11] +
       (int)param_1[4] + (int)param_1[0x20] + (int)param_1[0x10] == 0x5d0) {
     local_c = local_c + 1;
  }
  if ((int)param_1[0x13] +
       (int)param_1[0x19] + (int)param_1[0xd] + (int)param_1[0x23] + (int)param_1[8] +
       (int)param_1[0x1e] + (int)param_1[0x20] + (int)param_1[0x26] + (int)param_1[0x1e] +
       (int)param_1[0x23] + (int)param_1[0x28] == 0x354) {
     local_c = local_c + 1;
  }
  if ((int)param_1[0xd] +
       (int)param_1[0x25] + (int)param_1[4] + (int)param_1[0x27] + (int)param_1[0xe] +
       (int)param_1[0x1d] + (int)param_1[0x13] + (int)param_1[0x1d] == 0x20f) {
     local_c = local_c + 1;
  }
  if ((int)param_1[0x1b] +
       (int)param_1[0x10] + (int)param_1[9] + (int)param_1[0x20] + (int)param_1[0xe] +
       (int)param_1[7] + (int)param_1[0xc] == 0x1dd) {
     local_c = local_c + 1;
  }
  if ((int)param_1[6] + (int)param_1[9] == 0x9d) {
     local_c = local_c + 1;
  }
  if ((int)param_1[0x22] + (int)param_1[0xb] + (int)param_1[0xe] == 0xd6) {
     local_c = local_c + 1;
  }
  if ((int)param_1[0x29] +
       (int)param_1[0x16] + (int)param_1[0x26] + (int)param_1[0x1e] + (int)param_1[0x27] == 0x17e) {
     local_c = local_c + 1;
  }
  return local_c == 0x2a;
}

On looking at the above code, we can understand that it only returns 1, if it passes all the conditions. Now, it is practically not feasible to manually determine all the correct characters of the input (param_1), and moreover, all of these checks are simple arithmetic operations. So, we can leverage z3 in this case, to get the correct value of input.

First, of all, we will import z3 and initialize the Solver() function

1
2
3

from z3 import *

s= Solver()

Now, we need to initialize a variable, whose value is to be calculated, and here it is to be done using BitVec()

1

param_1= [BitVec(f'param_1[{i}]', 8) for i in range(42)]

It basically intializes an array, with each character of 8 bits..(enough to represent a character)
Now, we will add all the constraints using the add() function -

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86

s.add(param_1[0x1a] + param_1[0x20] + param_1[1] + param_1[0x29] ==0x183)
s.add(param_1[2] +param_1[10] + param_1[0xb] + param_1[0] + param_1[0x17] + param_1[0x1b]== 0x1ca )
 
s.add(param_1[0x13] +param_1[0x17] + param_1[3] + param_1[0x14] + param_1[0x1f] +param_1[0xd] + param_1[10] + param_1[0x21] + param_1[0x24] +param_1[0x23] + param_1[6] + param_1[9] + param_1[0x1e] +param_1[0x16] + param_1[7] + param_1[0x18] + param_1[0x27] +param_1[0x22] == 0x51a )
  
s.add(param_1[0x13] + param_1[0x27] + param_1[0xd] + param_1[0x11] == 0xcb )
 
s.add(param_1[0x1f] +param_1[0x1b] + param_1[4] + param_1[0x29] + param_1[8] +param_1[0x17] == 500 )
 
s.add(param_1[4] + param_1[0x1d] + param_1[0x22] + param_1[0x1e] == 0x170 )
 
s.add(param_1[0x25] +param_1[0x24] + param_1[0x23] + param_1[0x29] + param_1[0xf] +param_1[0x15] + param_1[0x28] + param_1[0x1c] + param_1[0x1a] +param_1[0x21] == 0x2fe )
  
s.add(param_1[0x15] +param_1[6] + param_1[10] + param_1[0xb] + param_1[0xf] + param_1[9] +param_1[0x1b] + param_1[3] + param_1[0x1b] + param_1[2] +param_1[0x26] == 0x33d )
 
s.add(param_1[0x1e] +param_1[0x1e] + param_1[0x23] + param_1[0x27] + param_1[0x19] +param_1[0] + param_1[0x29] + param_1[0x16] + param_1[0x17] + param_1[2]+ param_1[0] + param_1[0xb] + param_1[0x21] + param_1[0xc] + param_1[2]+ param_1[0x28] + param_1[0x15] + param_1[0x1c] + param_1[1] +param_1[0x16] == 0x65f )
 
s.add(param_1[0xb] +param_1[0x1e] + param_1[0x17] + param_1[0x21] + param_1[0x24] +param_1[0xc] + param_1[0] + param_1[0x23] + param_1[0] + param_1[3] +param_1[0xb] + param_1[0x21] + param_1[8] + param_1[0x22] +param_1[0xf] + param_1[0x1f] + param_1[2] == 0x57d )
 
s.add(param_1[0x22] +param_1[0x21] + param_1[0x29] + param_1[8] + param_1[0x29] +param_1[5] + param_1[0x10] == 0x289 )
 
s.add(param_1[0x1b] +param_1[0x24] + param_1[8] + param_1[3] + param_1[4] + param_1[0x1c]+ param_1[0x23] + param_1[0x23] + param_1[0x19] + param_1[0x15] +param_1[0x16] + param_1[0x28] == 0x373 )
 
s.add(param_1[0x1d] +param_1[0x22] * 2 + param_1[0xe] + param_1[0x29] + param_1[0x1e] +param_1[0x22] + param_1[0xc] + param_1[0xc] + param_1[0x20] +param_1[0x23] + param_1[0xc] + param_1[1] + param_1[1] +param_1[0x1c] + param_1[0x10] == 0x572 )
 
s.add(param_1[9] + param_1[0x14] + param_1[6] + param_1[1] == 0x16c )
 
s.add(param_1[0x1c] + param_1[9] == 0x65 )

  
s.add(param_1[0x25] +param_1[10] + param_1[0x10] + param_1[0x20] + param_1[0x27] +param_1[1] + param_1[0x27] + param_1[9] + param_1[0x29] +param_1[0x16] + param_1[0xf] + param_1[0x29] + param_1[0xf] +param_1[0x20] + param_1[0xb] + param_1[0x17] + param_1[0x21] +param_1[0x25] == 0x5f2 )
 
s.add(param_1[4] +param_1[0x17] + param_1[0x11] + param_1[0x15] + param_1[0x1b] +param_1[2] + param_1[0x1d] + param_1[1] + param_1[0x1d] +param_1[0x12] + param_1[0x10] + param_1[0xc] + param_1[0x11] +param_1[0x24] + param_1[0x13] == 0x3cb )
 
s.add(param_1[10] + param_1[10] + param_1[0x25] + param_1[0xd] == 0x156 )
 
s.add(param_1[8] +param_1[0xb] + param_1[0x29] + param_1[0x1d] + param_1[0x12] +param_1[0xc] + param_1[0x29] == 600 )
 
s.add(param_1[8] +param_1[0x21] + param_1[6] + param_1[0x14] + param_1[0x20] +param_1[0x1d] + param_1[0x28] + param_1[0x16] + param_1[0x11] +param_1[0x13] + param_1[0x24] + param_1[0x25] + param_1[0x1d] +param_1[0] + param_1[0x16] + param_1[9] + param_1[0x1b] == 0x4e7 )
 
s.add(param_1[0] +param_1[3] + param_1[0x20] + param_1[0xb] + param_1[4] +param_1[0x1e] == 0x247 )
 
s.add(param_1[0x1b] +param_1[0x21] + param_1[0x20] + param_1[0x1c] + param_1[0x25] +param_1[0x29] + param_1[0x28] + param_1[0x15] == 0x2a0 )
 
s.add(param_1[0x15] + param_1[0x10] + param_1[0x1e] + param_1[0x27] == 0x100 )
 
s.add(param_1[0x23] +param_1[5] + param_1[0x20] + param_1[0x28] + param_1[0x10] == 0x162 )
  
s.add(param_1[0x1e] +param_1[8] + param_1[0xb] + param_1[0x1d] + param_1[0x1f] +param_1[6] == 0x1c5)
s.add(param_1[0x29] + param_1[0x24] == 0xad )
 
s.add(param_1[10] + param_1[0x15] + param_1[0x14] + param_1[0xc] == 0x15d )
 
s.add(param_1[5] + param_1[0x1c] == 0x5e )
 
s.add(param_1[1] +param_1[0x18] + param_1[0x29] + param_1[4] + param_1[1] + param_1[2]+ param_1[0x18] + param_1[9] + param_1[0x1c] + param_1[0xd] +param_1[0x26] + param_1[0x21] + param_1[0x1c] + param_1[0x26] +param_1[7] + param_1[0x19] + param_1[0] + param_1[9] + param_1[0x1d] +param_1[0xc] == 0x64e )
 
s.add(param_1[0x28] +param_1[9] + param_1[0x18] + param_1[0x10] + param_1[0xf] +param_1[9] + param_1[0x22] + param_1[0xb] + param_1[0x23] +param_1[0x21] + param_1[0x21] + param_1[2] + param_1[0x1a] +param_1[0x11] + param_1[8] == 0x48c )
 
s.add(param_1[2] +param_1[2] + param_1[0x12] + param_1[0x1b] + param_1[0x12] +param_1[0x10] + param_1[0x29] + param_1[2] + param_1[0x24] +param_1[2] + param_1[0x16] + param_1[0x16] == 0x35c )
 
s.add(param_1[0xd] + param_1[0xe] + param_1[0xd] == 0x93 )
 
s.add(param_1[5] +param_1[0x1b] + param_1[0x18] + param_1[0x26] + param_1[0x27] +param_1[0x28] + param_1[0x16] + param_1[0x28] == 0x232 )
 
s.add(param_1[0x1e] +param_1[0x1a] + param_1[9] + param_1[0x1c] + param_1[0x14] +param_1[0xf] + param_1[0x12] + param_1[2] + param_1[0x1a] +param_1[5] + param_1[0x1e] == 0x315 )
 
s.add(param_1[0x17] +param_1[0x20] + param_1[0x13] + param_1[0x15] + param_1[2] +param_1[0x1c] + param_1[0x1b] + param_1[0x1b] + param_1[2] +param_1[0x27] + param_1[0x13] + param_1[0x27] + param_1[0x10] +param_1[2] + param_1[2] + param_1[0x18] + param_1[1] + param_1[0x1f]+ param_1[9] == 0x52d )
 
s.add(param_1[0xc] +param_1[0x26] + param_1[10] + param_1[0x14] + param_1[0x28] +param_1[0x1d] + param_1[0x26] + param_1[0x1a] + param_1[0x1a] +param_1[0x1f] + param_1[0x25] + param_1[0x14] + param_1[0xe] +param_1[10] + param_1[0x11] + param_1[0x26] + param_1[0x11] +param_1[4] + param_1[0x20] + param_1[0x10] == 0x5d0 )

  
s.add(param_1[0x13] +param_1[0x19] + param_1[0xd] + param_1[0x23] + param_1[8] +param_1[0x1e] + param_1[0x20] + param_1[0x26] + param_1[0x1e] +param_1[0x23] + param_1[0x28] == 0x354 )
 
s.add(param_1[0xd] +param_1[0x25] + param_1[4] + param_1[0x27] + param_1[0xe] +param_1[0x1d] + param_1[0x13] + param_1[0x1d] == 0x20f )
 
s.add(param_1[0x1b] +param_1[0x10] + param_1[9] + param_1[0x20] + param_1[0xe] +param_1[7] + param_1[0xc] == 0x1dd )
 
s.add(param_1[6] + param_1[9] == 0x9d)
 
s.add(param_1[0x22] + param_1[0xb] + param_1[0xe] == 0xd6 )
 
s.add(param_1[0x29] +param_1[0x16] + param_1[0x26] + param_1[0x1e] + param_1[0x27] == 0x17e )

for i in range(42):
    s.add(32<param_1[i], param_1[i]<127) # check for the characters to be in printable range

After this, we just need to check, whether all the conditions are satisfiable or not and if there exists a solution, and print out the output. We can use the model() function to inspect the values assigned to each variable that satisfies the constraints.

1
2
3
4
5
6
7
8
9

if s.check()==sat:
    m = s.model()
    #print(m)
    print("Flag : " , end='')
    for i in range(42):
        print(chr(m[param_1[i]].as_long()), end='')

else:
    print("Failed to find the flag")

So here’s the complete code -

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103

from z3 import *

s= Solver()

param_1= [BitVec(f'param_1[{i}]', 8) for i in range(42)]
s.add(param_1[0x1a] + param_1[0x20] + param_1[1] + param_1[0x29] ==0x183)
s.add(param_1[2] +param_1[10] + param_1[0xb] + param_1[0] + param_1[0x17] + param_1[0x1b]== 0x1ca )
 
s.add(param_1[0x13] +param_1[0x17] + param_1[3] + param_1[0x14] + param_1[0x1f] +param_1[0xd] + param_1[10] + param_1[0x21] + param_1[0x24] +param_1[0x23] + param_1[6] + param_1[9] + param_1[0x1e] +param_1[0x16] + param_1[7] + param_1[0x18] + param_1[0x27] +param_1[0x22] == 0x51a )
  
s.add(param_1[0x13] + param_1[0x27] + param_1[0xd] + param_1[0x11] == 0xcb )
 
s.add(param_1[0x1f] +param_1[0x1b] + param_1[4] + param_1[0x29] + param_1[8] +param_1[0x17] == 500 )
 
s.add(param_1[4] + param_1[0x1d] + param_1[0x22] + param_1[0x1e] == 0x170 )
 
s.add(param_1[0x25] +param_1[0x24] + param_1[0x23] + param_1[0x29] + param_1[0xf] +param_1[0x15] + param_1[0x28] + param_1[0x1c] + param_1[0x1a] +param_1[0x21] == 0x2fe )
  
s.add(param_1[0x15] +param_1[6] + param_1[10] + param_1[0xb] + param_1[0xf] + param_1[9] +param_1[0x1b] + param_1[3] + param_1[0x1b] + param_1[2] +param_1[0x26] == 0x33d )
 
s.add(param_1[0x1e] +param_1[0x1e] + param_1[0x23] + param_1[0x27] + param_1[0x19] +param_1[0] + param_1[0x29] + param_1[0x16] + param_1[0x17] + param_1[2]+ param_1[0] + param_1[0xb] + param_1[0x21] + param_1[0xc] + param_1[2]+ param_1[0x28] + param_1[0x15] + param_1[0x1c] + param_1[1] +param_1[0x16] == 0x65f )
 
s.add(param_1[0xb] +param_1[0x1e] + param_1[0x17] + param_1[0x21] + param_1[0x24] +param_1[0xc] + param_1[0] + param_1[0x23] + param_1[0] + param_1[3] +param_1[0xb] + param_1[0x21] + param_1[8] + param_1[0x22] +param_1[0xf] + param_1[0x1f] + param_1[2] == 0x57d )
 
s.add(param_1[0x22] +param_1[0x21] + param_1[0x29] + param_1[8] + param_1[0x29] +param_1[5] + param_1[0x10] == 0x289 )
 
s.add(param_1[0x1b] +param_1[0x24] + param_1[8] + param_1[3] + param_1[4] + param_1[0x1c]+ param_1[0x23] + param_1[0x23] + param_1[0x19] + param_1[0x15] +param_1[0x16] + param_1[0x28] == 0x373 )
 
s.add(param_1[0x1d] +param_1[0x22] * 2 + param_1[0xe] + param_1[0x29] + param_1[0x1e] +param_1[0x22] + param_1[0xc] + param_1[0xc] + param_1[0x20] +param_1[0x23] + param_1[0xc] + param_1[1] + param_1[1] +param_1[0x1c] + param_1[0x10] == 0x572 )
 
s.add(param_1[9] + param_1[0x14] + param_1[6] + param_1[1] == 0x16c )
 
s.add(param_1[0x1c] + param_1[9] == 0x65 )

  
s.add(param_1[0x25] +param_1[10] + param_1[0x10] + param_1[0x20] + param_1[0x27] +param_1[1] + param_1[0x27] + param_1[9] + param_1[0x29] +param_1[0x16] + param_1[0xf] + param_1[0x29] + param_1[0xf] +param_1[0x20] + param_1[0xb] + param_1[0x17] + param_1[0x21] +param_1[0x25] == 0x5f2 )
 
s.add(param_1[4] +param_1[0x17] + param_1[0x11] + param_1[0x15] + param_1[0x1b] +param_1[2] + param_1[0x1d] + param_1[1] + param_1[0x1d] +param_1[0x12] + param_1[0x10] + param_1[0xc] + param_1[0x11] +param_1[0x24] + param_1[0x13] == 0x3cb )
 
s.add(param_1[10] + param_1[10] + param_1[0x25] + param_1[0xd] == 0x156 )
 
s.add(param_1[8] +param_1[0xb] + param_1[0x29] + param_1[0x1d] + param_1[0x12] +param_1[0xc] + param_1[0x29] == 600 )
 
s.add(param_1[8] +param_1[0x21] + param_1[6] + param_1[0x14] + param_1[0x20] +param_1[0x1d] + param_1[0x28] + param_1[0x16] + param_1[0x11] +param_1[0x13] + param_1[0x24] + param_1[0x25] + param_1[0x1d] +param_1[0] + param_1[0x16] + param_1[9] + param_1[0x1b] == 0x4e7 )
 
s.add(param_1[0] +param_1[3] + param_1[0x20] + param_1[0xb] + param_1[4] +param_1[0x1e] == 0x247 )
 
s.add(param_1[0x1b] +param_1[0x21] + param_1[0x20] + param_1[0x1c] + param_1[0x25] +param_1[0x29] + param_1[0x28] + param_1[0x15] == 0x2a0 )
 
s.add(param_1[0x15] + param_1[0x10] + param_1[0x1e] + param_1[0x27] == 0x100 )
 
s.add(param_1[0x23] +param_1[5] + param_1[0x20] + param_1[0x28] + param_1[0x10] == 0x162 )
  
s.add(param_1[0x1e] +param_1[8] + param_1[0xb] + param_1[0x1d] + param_1[0x1f] +param_1[6] == 0x1c5)
s.add(param_1[0x29] + param_1[0x24] == 0xad )
 
s.add(param_1[10] + param_1[0x15] + param_1[0x14] + param_1[0xc] == 0x15d )
 
s.add(param_1[5] + param_1[0x1c] == 0x5e )
 
s.add(param_1[1] +param_1[0x18] + param_1[0x29] + param_1[4] + param_1[1] + param_1[2]+ param_1[0x18] + param_1[9] + param_1[0x1c] + param_1[0xd] +param_1[0x26] + param_1[0x21] + param_1[0x1c] + param_1[0x26] +param_1[7] + param_1[0x19] + param_1[0] + param_1[9] + param_1[0x1d] +param_1[0xc] == 0x64e )
 
s.add(param_1[0x28] +param_1[9] + param_1[0x18] + param_1[0x10] + param_1[0xf] +param_1[9] + param_1[0x22] + param_1[0xb] + param_1[0x23] +param_1[0x21] + param_1[0x21] + param_1[2] + param_1[0x1a] +param_1[0x11] + param_1[8] == 0x48c )
 
s.add(param_1[2] +param_1[2] + param_1[0x12] + param_1[0x1b] + param_1[0x12] +param_1[0x10] + param_1[0x29] + param_1[2] + param_1[0x24] +param_1[2] + param_1[0x16] + param_1[0x16] == 0x35c )
 
s.add(param_1[0xd] + param_1[0xe] + param_1[0xd] == 0x93 )
 
s.add(param_1[5] +param_1[0x1b] + param_1[0x18] + param_1[0x26] + param_1[0x27] +param_1[0x28] + param_1[0x16] + param_1[0x28] == 0x232 )
 
s.add(param_1[0x1e] +param_1[0x1a] + param_1[9] + param_1[0x1c] + param_1[0x14] +param_1[0xf] + param_1[0x12] + param_1[2] + param_1[0x1a] +param_1[5] + param_1[0x1e] == 0x315 )
 
s.add(param_1[0x17] +param_1[0x20] + param_1[0x13] + param_1[0x15] + param_1[2] +param_1[0x1c] + param_1[0x1b] + param_1[0x1b] + param_1[2] +param_1[0x27] + param_1[0x13] + param_1[0x27] + param_1[0x10] +param_1[2] + param_1[2] + param_1[0x18] + param_1[1] + param_1[0x1f]+ param_1[9] == 0x52d )
 
s.add(param_1[0xc] +param_1[0x26] + param_1[10] + param_1[0x14] + param_1[0x28] +param_1[0x1d] + param_1[0x26] + param_1[0x1a] + param_1[0x1a] +param_1[0x1f] + param_1[0x25] + param_1[0x14] + param_1[0xe] +param_1[10] + param_1[0x11] + param_1[0x26] + param_1[0x11] +param_1[4] + param_1[0x20] + param_1[0x10] == 0x5d0 )

  
s.add(param_1[0x13] +param_1[0x19] + param_1[0xd] + param_1[0x23] + param_1[8] +param_1[0x1e] + param_1[0x20] + param_1[0x26] + param_1[0x1e] +param_1[0x23] + param_1[0x28] == 0x354 )
 
s.add(param_1[0xd] +param_1[0x25] + param_1[4] + param_1[0x27] + param_1[0xe] +param_1[0x1d] + param_1[0x13] + param_1[0x1d] == 0x20f )
 
s.add(param_1[0x1b] +param_1[0x10] + param_1[9] + param_1[0x20] + param_1[0xe] +param_1[7] + param_1[0xc] == 0x1dd )
 
s.add(param_1[6] + param_1[9] == 0x9d)
 
s.add(param_1[0x22] + param_1[0xb] + param_1[0xe] == 0xd6 )
 
s.add(param_1[0x29] +param_1[0x16] + param_1[0x26] + param_1[0x1e] + param_1[0x27] == 0x17e )

for i in range(42):
    s.add(32<param_1[i], param_1[i]<127)

#print(s.check())

if s.check()==sat:
    m = s.model()
    #print(m)
    print("Flag : " , end='')
    for i in range(42):
        print(chr(m[param_1[i]].as_long()), end='')

else:
    print("Failed to find the flag")

On running the code, we get the flag -

flag

Similarly let’s look at another challenge.

Example 2

This is a reverse engineering challenge from the UIUCTF 2024

You can acess the challenge file here
The challenge description says -

desc

On opening the binary in Ghidra, we have the main function as - 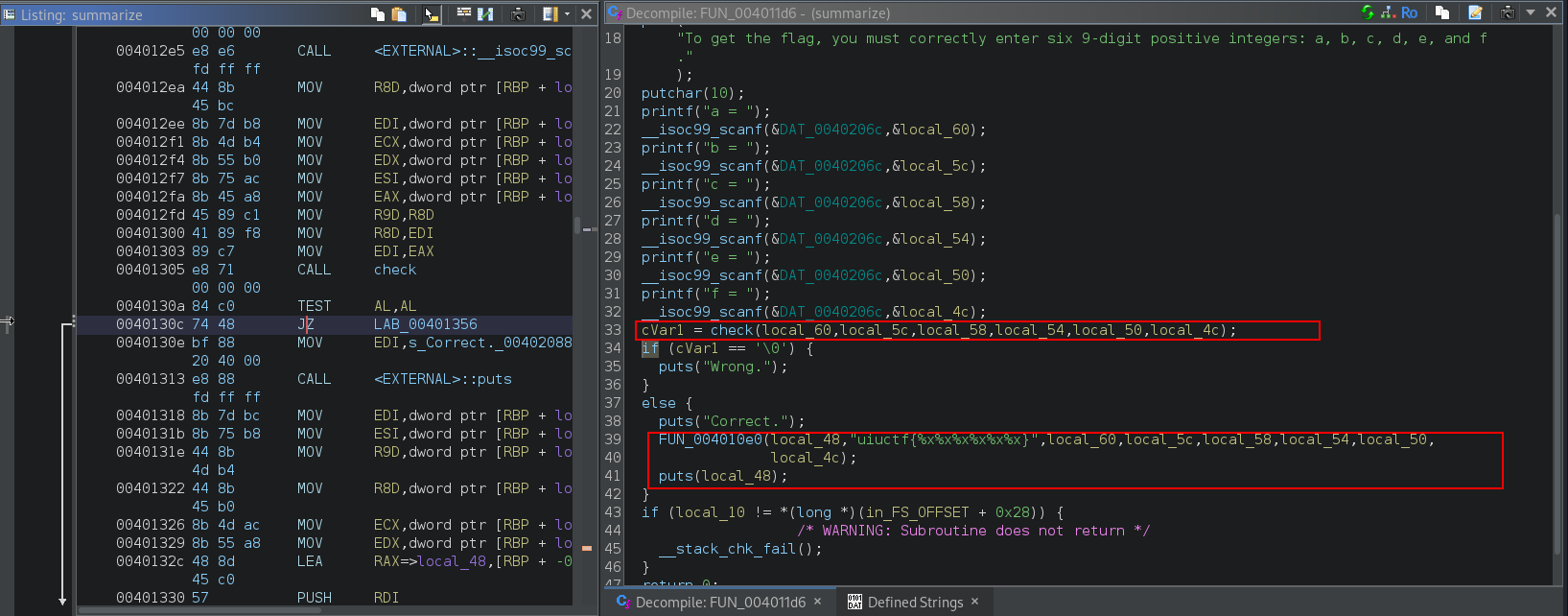main

It is taking 6 integer inputs, each of 9 digits, and passing our inputs to a function check (I renamed the function). If the function returns 0, it prints “wrong”, else it gives us the flag, according to our input. So, here we can’t just bypass the check, we need to get the correct input. Let’s check the check function -

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

undefined4 check(uint param_1,uint param_2,uint param_3,uint param_4,uint param_5,uint param_6)

{
  undefined4 uVar1;
  uint uVar2;
  uint uVar3;
  undefined4 uVar4;
  uint uVar5;
  uint uVar6;
  uint uVar7;
  uint uVar8;
  uint uVar9;
  uint uVar10;
  ulong uVar11;
  
  if (((((param_1 < 0x5f5e101) || (param_2 < 0x5f5e101)) || (param_3 < 0x5f5e101)) ||
      ((param_4 < 0x5f5e101 || (param_5 < 0x5f5e101)))) || (param_6 < 100000001)) {
    uVar1 = 0;
  }
  else if (((param_1 < 1000000000) && (param_2 < 1000000000)) &&
          ((param_3 < 1000000000 &&
           (((param_4 < 1000000000 && (param_5 < 1000000000)) && (param_6 < 1000000000)))))) {
    uVar1 = sub(param_1,param_2);
    uVar2 = add(uVar1,param_3);
    uVar3 = add(param_1,param_2);
    uVar1 = multiply(2,param_2);
    uVar4 = multiply(3,param_1);
    uVar5 = sub(uVar4,uVar1);
    uVar6 = xor(param_1,param_4);
    uVar1 = add(param_3,param_1);
    uVar7 = bitwise_and(param_2,uVar1);
    uVar11 = add(param_2,param_4);
    uVar1 = add(param_4,param_6);
    uVar8 = xor(param_3,uVar1);
    uVar9 = sub(param_5,param_6);
    uVar10 = add(param_5,param_6);
    if ((((uVar2 % 0x10ae961 == 0x3f29b9) && (uVar3 % 0x1093a1d == 0x8bdcd2)) &&
        ((uVar5 % uVar6 == 0x212c944d &&
         ((uVar7 % 0x6e22 == 0x31be && ((int)((uVar11 & 0xffffffff) % (ulong)param_1) == 0x2038c43c)
          ))))) &&
       ((uVar8 % 0x1ce628 == 0x1386e2 &&
        ((uVar9 % 0x1172502 == 0x103cf4f && (uVar10 % 0x2e16f83 == 0x16ab0d7)))))) {
      uVar1 = 1;
    }
    else {
      uVar1 = 0;
    }
  }
  else {
    uVar1 = 0;
  }
  return uVar1;
}

NOTE : I renamed the functions - sub, add, multiply etc…

We can see that, first of all it is checking that whether our input is an integer of 9 digits or not. Then it is passing our input into other functions and doing some calculations. Let’s take a look at multiply function -

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

int multiply(uint param_1,int param_2)

{
  byte bVar1;
  uint local_1c;
  int local_14;
  
  local_14 = 0;
  bVar1 = 0;
  for (local_1c = param_1; local_1c != 0; local_1c = local_1c >> 1) {
    local_14 = local_14 + (param_2 << (bVar1 & 0x1f)) * (local_1c & 1);
    bVar1 = bVar1 + 1;
  }
  return local_14;
}

It looks complex right..!! On running the above function as a C program, I observed that it is actually just performing simple mulitplication. Similarly I did it for the other functions and renamed them accordingly for better understanding.
Now, as we have transformed all the operations into simple arithmetic, logical operations, we can now use z3 to calculate the 6 integers similarly as we did in the previous example.
Here is the code for it -

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65

from z3 import *

def addition(a,b):
    return a+b
def multiply(a,b):
    return a*b
def sub(a,b):
    return a-b
def xor(a,b):
    return a^b
def bitwise_and(a,b):
    return a & b
s= Solver()

# Initializatin using tuple unpacking
a, b, c, d, e, f = BitVecs('a b c d e f', 32)

s.add(a < 1000000000)
s.add(b < 1000000000)
s.add(c < 1000000000) 
s.add(d < 1000000000)
s.add(e < 1000000000)
s.add(f < 1000000000)
s.add(a > 100000001)
s.add(b > 100000001)
s.add(c > 100000001)
s.add(d > 100000001)
s.add(e > 100000001)
s.add(f > 100000001)


uVar1 = sub(a,b)
uVar2 = addition(uVar1,c)
uVar3 = addition(a,b)
uVar1 = multiply(2,b)
uVar4 = multiply(3,a)
uVar5 = sub(uVar4,uVar1)
uVar6 = xor(a,d)
uVar1 = addition(c,a)
uVar7 = bitwise_and(b,uVar1)
uVar11 = addition(b,d)
uVar1 = addition(d,f)
uVar8 = xor(c,uVar1)
uVar9 = sub(e,f)
uVar10 = addition(e,f)

s.add(
    (uVar2 % 0x10ae961 == 0x3f29b9) &
    (uVar3 % 0x1093a1d == 0x8bdcd2) &
    (uVar5 % uVar6 == 0x212c944d) &
    (uVar7 % 0x6e22 == 0x31be) &
    ((uVar11 & 0xffffffff) % a == 0x2038c43c) &
    (uVar8 % 0x1ce628 == 0x1386e2) &
    (uVar9 % 0x1172502 == 0x103cf4f) &
    (uVar10 % 0x2e16f83 == 0x16ab0d7)
)
# print(s.check())

arr=[a,b,c,d,e,f]
if s.check()== sat:
    m= s.model()
    for i in arr:
        print(f'{i}', ':', m[i])

Now, on running the above code, we get all the 6 integers, and on passing it as an input to the binary, we get our flag.

Stay tuned for more articles..Happy Hacking !!

Blogs
Z3 Reverse Engineering
This post is licensed under CC BY 4.0 by the author.